数据结构
数组
几乎所有的编程语言都原生支持数组类型,因为数组是最简单的内存数据结构。数组存储一系列同一种数据类型的值。虽然在 JavaScript 里,也可以在数组中保存不同类型的值,但我们还是遵守最佳实践,避免这么做(大多数语言都没有这个能力)。
Tip:通过 push 和pop方法,就能用数组来模拟栈。
let numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log('原数组', numbers);
numbers.push(11);
console.log('在数组末尾插入11', numbers)
numbers.pop();
console.log('在数组末尾删除一个元素', numbers)
Tip: 通过 shift 和 unshift 方法,我们就能用数组模拟基本的队列数据结构。
let numbers = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log('原数组', numbers);
numbers.unshift(-2)
console.log('在数组开头插入-2', numbers)
numbers.shift();
console.log('在数组开头删除一个元素', numbers)
栈
栈是一种遵从后进先出(LIFO)原则的有序集合。新添加或待删除的元素都保存在栈的同一端,称作栈顶,另一端就叫栈底。在栈里,新元素都靠近栈顶,旧元素都接近栈底。
在现实生活中也能发现很多栈的例子。例如,下图里的一摞书或者餐厅里叠放的盘子。

利用数组创建一个栈
// LIFO:只能用 push, pop 方法添加和删除栈中元素,满足 LIFO 原则
class Stack {
constructor() {
this.items = [];
}
/**
* @description 向栈添加元素,该方法只添加元素到栈顶,也就是栈的末尾。
* @param {*} element
* @memberof Stack
*/
push(element) {
this.items.push(element);
}
/**
* @description 从栈移除元素
* @returns 移出最后添加进去的元素
* @memberof Stack
*/
pop() {
return this.items.pop();
}
/**
* @description 查看栈顶元素
* @returns 返回栈顶的元素
* @memberof Stack
*/
peek() {
return this.items[this.items.length - 1];
}
/**
* @description 检查栈是否为空
* @returns
* @memberof Stack
*/
isEmpty() {
return this.items.length === 0;
}
/**
* @description 返回栈的长度
* @returns
* @memberof Stack
*/
size() {
return this.items.length;
}
/**
* @description 清空栈元素
* @memberof Stack
*/
clear() {
this.items = [];
}
}
用栈解决问题
栈的实际应用非常广泛(只要满足 LIFO 规则的算法都可以使用栈来解决问题)。在回溯问题中,它可以存储访问过的任务或路径、撤销的操作。Java 和 C# 用栈来存储变量和方法调用,特别是处理递归算法时,有可能抛出一个栈溢出异常。
利用栈解决十进制转二进制的问题。
/**
* 把十进制转换成二进制。
* @param {*} decNumber 十进制
*/
export function decimalToBinary(decNumber) {
const remStack = new Stack();
let number = decNumber; // 十进制数字
let rem; // 余数
let binaryString = '';
while (number > 0) {
// 当结果不为0,获得一个余数
rem = Math.floor(number % base);
remStack.push(rem); // 入栈
number = Math.floor(number / base);
}
while(!remStack.isEmpty()) {
binaryString += remStack.pop().toString();
}
return binaryString;
}
代码运行方式——调用栈
调用栈,表示函数或子例程像堆积木一样存放,以实现层层调用。 下面以一段 Java 代码为例:
class Student {
int age;
String name;
public Student(int Age, String Name) {
this.age = Age;
setName(Name);
}
public void setName(String Name) {
this.name = Name;
}
}
public class Main {
public static void main(String[] args) {
Student s;
s = new Student(23, "Jonh")
}
}
上面这段代码运行的时候,首先调用 main 方法,里面需要生成一个 Student 的实例,于是又调用 Student 构造函数。在构造函数中,又调用到 setName 方法。
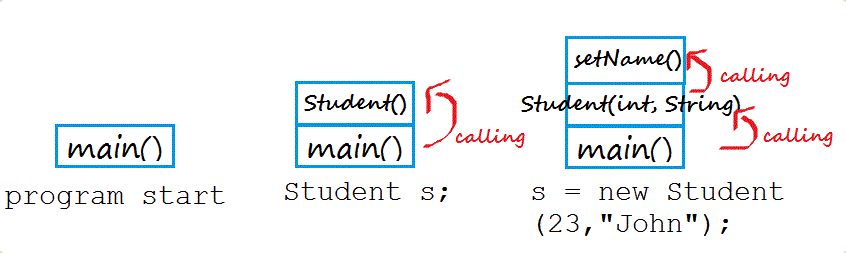
这三次调用像积木一样堆起来,就叫做“调用栈”。程序运行的时候,总是先完成最上层的调用,然后将它的值返回到下一层调用。直至完成整个调用栈,返回最后的结果。
原理大概:
- 调用 main 方法,这个时候需要调用 Student 构造函数,把这个位置A作为 return 地址存入栈中。
- 这个时候调用并进入 Student 构造函数内部,遇到 SetName() 方法,把这里的位置B 作为 return 地址存入栈中记录下来存入栈中。
- 这时调用并进入 setName() 方法内部执行完毕后,之后从栈中拿出 B 地址,返回到 Student 函数内部继续执行。
- Student 函数执行完毕后,然后从栈中继续拿出 A 地址,进入到一开始的 main 函数内部执行,至此完毕。
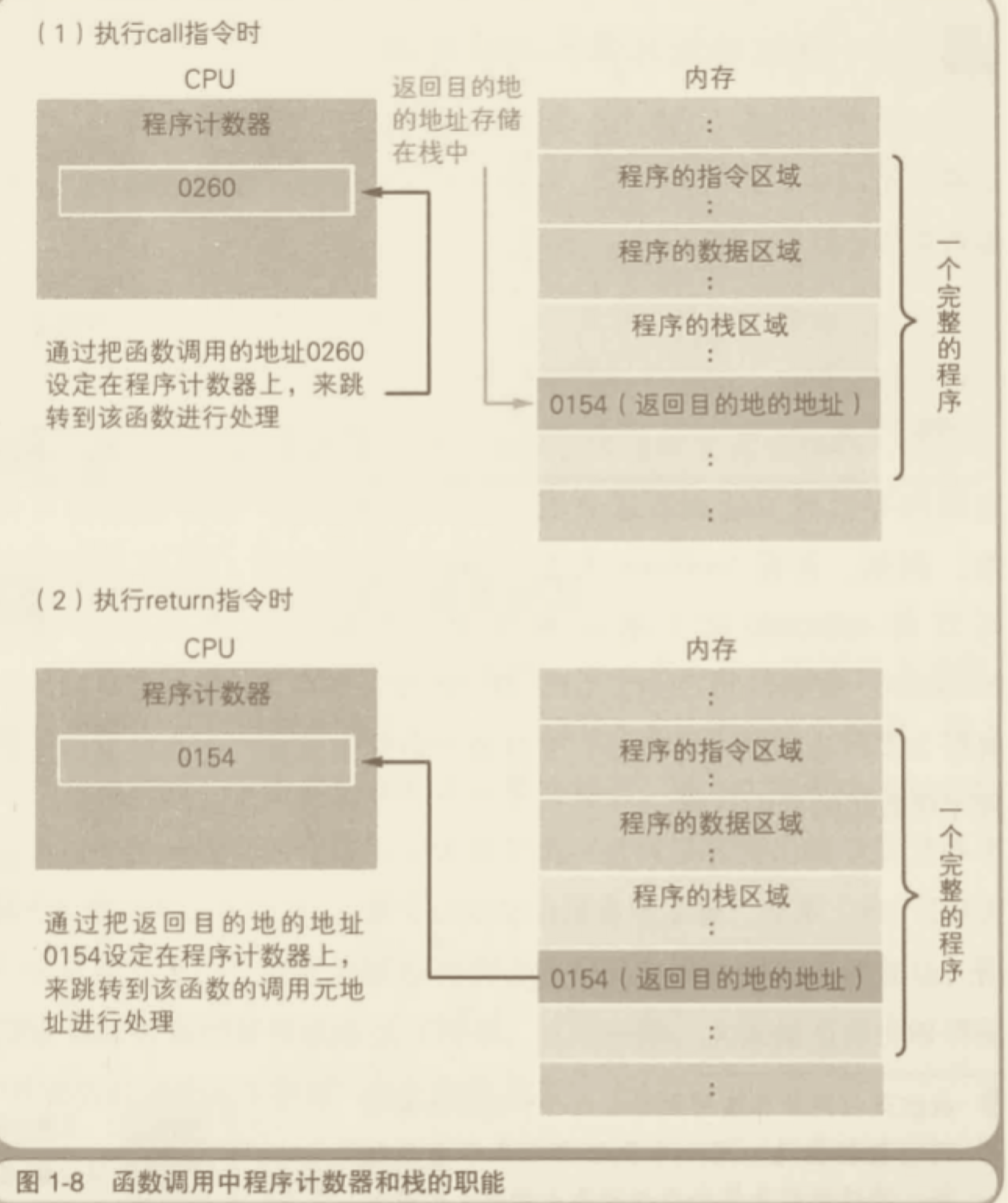
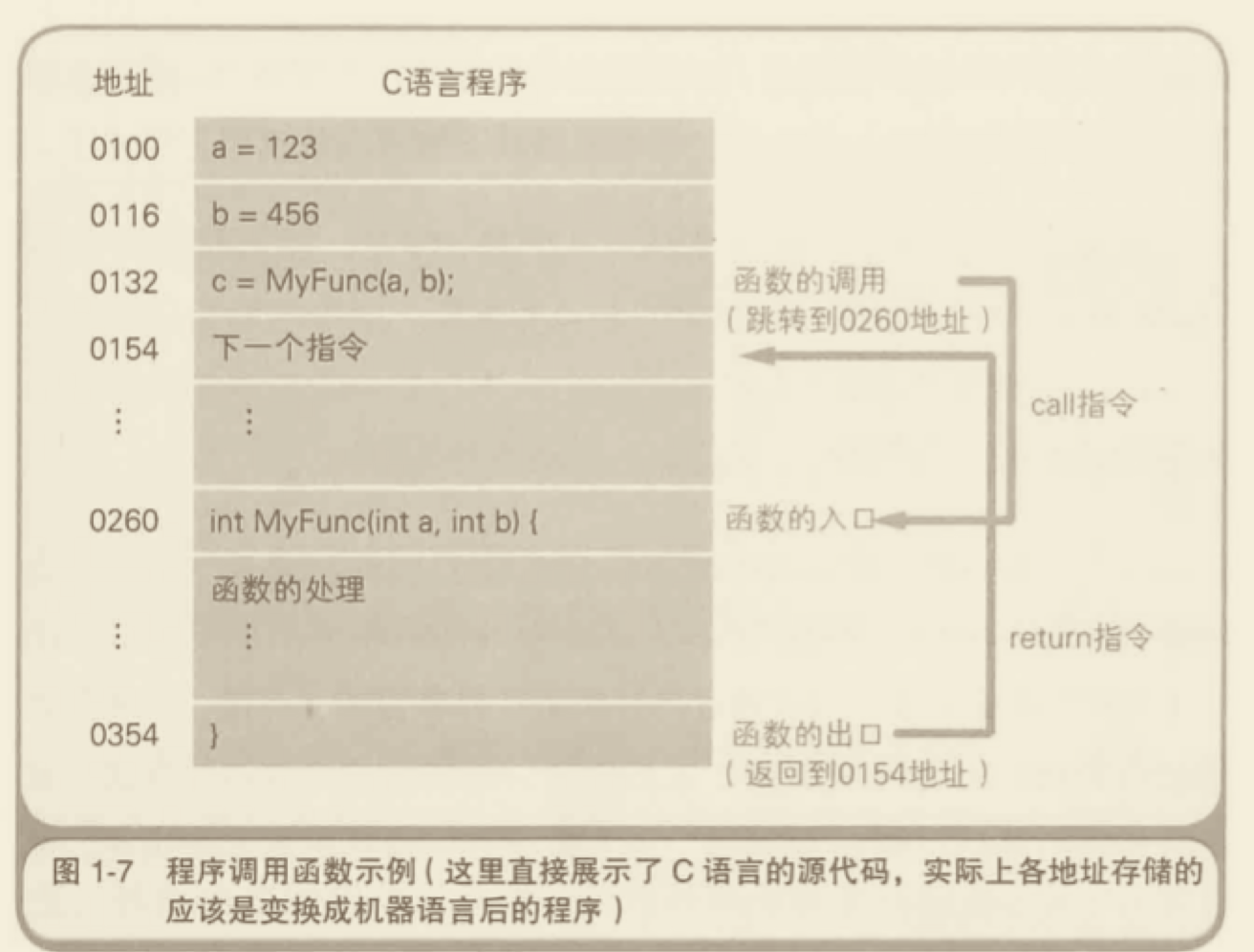
内存区域
程序运行的时候,需要内存空间存放数据。一般来说,系统会划分出两种不同的内存空间:一种是叫做 stack (栈),另一种叫做 heap(堆)。一般来说,每个线程分配一个 stack,每个进程分配一个 heap,也就是说,stack 是线程独占的,heap 是现场共享的。此外,stack 创建的时候,大小是确定的,数据超过这个带下,就发生 stack overflow 错误。而 heap 的大小是不确定的,需要的话可以不断增加。
栈由系统自动分配释放,存放函数的参数值合局部变量的值等。
堆一般由程序员分配释放,若程序员不释放,程序结束时可能由 OS 回收。
根据上面这些区别,数据存放的规则是:只要是局部的、占用空间确定的数据,一般都存放在 stack 里面,否则就放在 heap 里面。请看下面这段代码:
public void Method1() {
int i = 4;
int y = 2;
class1 cls1 = new class1();
}
上面的代码的 Method1 方法,共包含了三个变量:i,y 和 cls1。其中,i 和 y 的值是整数,内存占用空间是确定,而且是局部变量,只用在 Methods1 区块之内,不会用于区块之外。cls1 也是局部变量,但是类型为指针变量,指向一个对象的实例。指针变量占用的大小是确定的(这里存储的是地址),但是对象实例以目前的信息无法确知所占用的内存空间大小。
这三个变量合一个对象实例在内存中的存放方式如下:
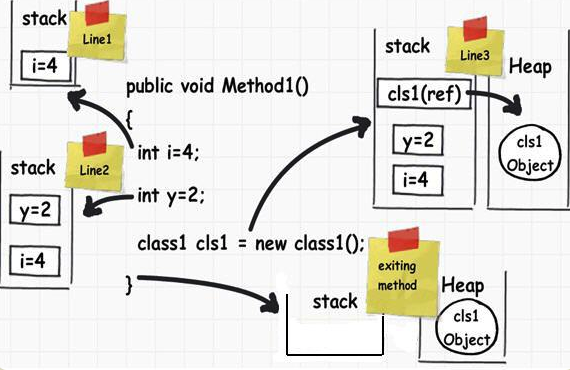
从上图可以看到,i、y 和 cls1 都存放在 stack,因为它们占用内存空间都是确定的,而且本身也属于局部变量。但是,cls1 指向的对象实例存放在 heap,因为它的大小不确定。
接下来的问题是,当 Method1 方法运行结束,会发生什么事?
回答是整个 stack 被清空,i、y 和 cls1 这三个变量消失,因为它们是局部变量,区块一旦运行结束,就没必要再存在了。而 heap 之中的哪个对象实例继续存在,直到系统的垃圾清理机制(garbage collector)将这块内存回收。因此,一般来说,内存泄漏都发生在 heap,即某些内存空间不再被使用了,却因为种种原因,没有被系统回收。
综合分析一段 JavaScript 代码(内存区域+调用栈)
递归算法中,变量和方法是如何入栈的,为什么有爆栈?或者说栈溢出?
- 调用栈
每当一个函数被一个算法调用时,该函数会进入调用栈的顶部。当使用递归时,每个函数调用都回堆叠在调用栈的顶部,这是因为每个调用都可能依赖前一个调用的结果。
/**
* 递归阶乘
* @param {*} n
*/
function factorial(n) {
console.trace()
if (n === 1 || n === 0) { // 基线条件
return 1;
}
return n * factorial(n -1); // 递归调用
}
console.log('factorial(3) :', factorial(3));
我们可以用浏览器看到调用栈的行为,如下图所示
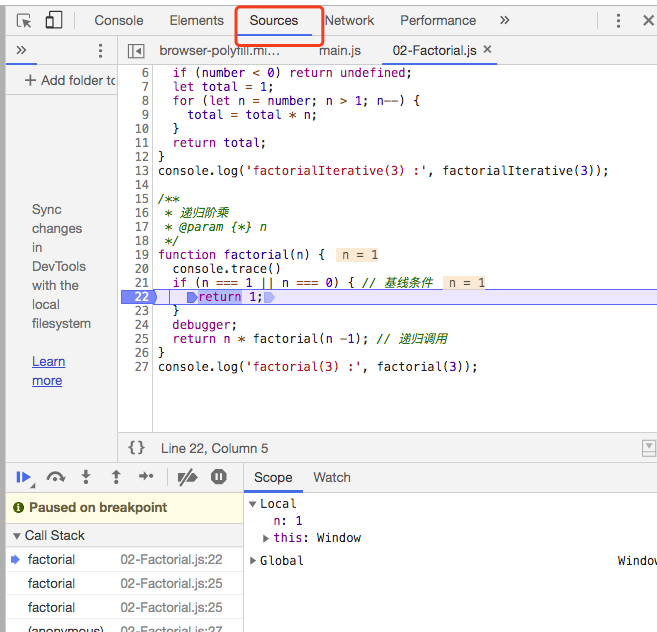
通过 debugger 可以看到每一次函数在推入栈,直接当 factorial(1) 被调用时,我们能在控制台得到下面的结果。
factorial @ 02-Factorial.js:20
factorial @ 02-Factorial.js:25
factorial @ 02-Factorial.js:25
当 factorial(1) 返回 1 时,调用栈开始弹出调用,返回结果,直到 3 * factorial(2) 被计算。
- JavaScirpt 调用栈大小的限制
如果忘记加上用以停止函数递归调用的基线条件,会发生什么呢?递归并不会无限地执行下去,浏览器会抛出错误,也就是所谓的栈溢出错误。(stack overflow error)。
每个浏览器都有自己的上限,可用以下代码测试。
// 测试浏览器的栈溢出错误,即超过最大调用栈
let i = 0;
function recursiveFn() {
i++;
recursiveFn();
}
try {
recursiveFn();
} catch (ex) {
console.log('i = ' + i + 'error: ' + ex);
}
在 Chrome 78 中,该函数执行了 15689 次,之后抛出错误 RangeError: Maximum call stack size exceeded(超限错误:超过最大调用栈大小)。
解决方案是可以使用尾递归优化。
队列
队列数据结构
队列是遵循先进先出(FIFO,也称为先来先服务)原则的一组有序的项。队列在尾部添加新元素,并从顶部移除元素。最新添加的元素必须排在队列的末尾。
在现实中,最常见的队列的例子就是排队。

在电影院、自助餐厅、杂货店收银台,我们都会排队。排在第一位的人会先接受服务。 在计算机科学中,一个常见的例子就是打印队列。比如说,我们需要打印五份文档。我们会打开每个文档,然后点击打印按钮。每个文档都会被发送至打印队列。第一个发送到打印队列的文档会首先被打印,以此类推,直到打印完所有文档。
创建队列
export default class Queue {
constructor() {
this.count = 0; // 控制队列的大小
this.lowestCount = 0; // 用于追踪第一元素,便于从队列前端移除元素
this.items = {}; // 用对象存储我们的元素
}
/**
* 向队列添加元素
* 该方法负责向队列添加新元素,新的项只能添加到队列末尾。
* @param {*} element
*/
enqueue(element) {
this.items[this.count] = element;
this.count++;
}
/**
* 从队列移除元素
*/
dequeue() {
if (this.isEmpty()) {
return undefined;
}
const result = this.items[this.lowestCount]; // 暂存队列头部的值,以便改元素被移除后将它返回
delete this.items[this.lowestCount];
this.lowestCount++; // 属性+ 1
return result;
}
/**
* 查看队列头元素
*/
peek() {
if (this.isEmpty()) {
return undefined;
}
return this.items[this.lowestCount];
}
/**
* 检查队列是否为空并获取它的长度
*/
isEmpty() {
return this.count - this.lowestCount === 0; // 要计算队列中有多少元素,我们只需要计算 count 和 lowestCount 之间的差值
}
/**
* 计算队列中有多少元素
*/
size() {
return this.count - this.lowestCount;
}
/**
* 清空队列
* 要清空队列,我们可以调用 dequeue 方法直到它返回 undefined,也可以简单地将队列中的舒心值重设为和构造函数的一样。
* @memberof Queue
*/
clear() {
this.items = {};
this.count = 0;
this.lowestCount = 0;
}
toString() {
if (this.isEmpty()) {
return '';
}
let objString = `${this.items[this.lowestCount]}`;
for (let i = this.lowestCount + 1; i < this.count; i++) {
objString = `${objString},${this.items[i]}`
}
return objString;
}
}
双端队列数据结构
使用队列和双端队列来解决问题
循环队列——击鼓传花游戏
import Queue from "../data-structures/queue"
/**
* 模拟击鼓传花
* 循环队列。在这个游戏中,孩子们围成一个圆圈,把花尽快传递给旁边的人。某一时刻传花停止,这个时候花在谁手上,谁就退出圆圈,结束游戏。
* 重复这个过程,直到只剩一个孩子(胜者)。
* @export
* @param {*} elementsList 要入列的元素
* @param {*} num // 达到给定的传递次数。 // 可以随机输入
*/
export default function hotPotato(elementsList, num) {
const queue = new Queue();
const elimitatedList = [];
for (let i = 0; i < elementsList.length; i++) {
queue.enqueue(elementsList[i]);
}
while (queue.size() > 1) {
// 循环队列,给定一个数字,然后迭代队列。从队列开头移除一项,再将其添加到队列末尾,模拟击鼓传花。
// 一旦达到给定的传递次数,拿着花的那个人就被淘汰了。(从队列中移除)
for (let i = 0; i < num; i++) {
queue.enqueue(queue.dequeue());
}
elimitatedList.push(queue.dequeue());
}
return {
elimitated: elimitatedList,
winner: queue.dequeue()
}
}
JavaScript 任务队列
当我们在浏览器中打开标签时,就会创建一个任务队列。这是因为每个标签都是单线程处理所有的任务,成为事件循环。浏览器要负责多个任务,如渲染 HTML、执行 JavaScript 代码、处理用户交互(用户输入、鼠标点击等)、执行和处理异步请求。
二叉堆和堆排序
二叉堆
堆(Heap)是计算机科学一类特殊的数据结构的统称,堆通常是一个可以看作一颗完全二叉树的数组对象。 二叉堆是一种特殊的二叉树,有一以下两个特性。
- 它是一颗完全二叉树,表示树的每一层都有左侧和右侧子节点。(除了最后一层的叶节点),并且最后一层的叶节点尽可能都是左侧子节点,这叫做结构特性。
- 二叉堆不是最小堆就是最大堆。最小堆允许你快速导出树的最小值,最大堆允许你快速导出树的最大值。所有的节点都大于等于(最大堆)或小于等于(最小堆)每个它的子节点。这叫做堆特性。
- 在二叉堆中,每个子节点都要大于等于父节点(最小堆)或小于等于父节点(最大堆)。 将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。 堆是非线性数据结构,相当于一维数组,有两个直接后继。
创建最小堆类
使用一个数组,通过索引值检索父节点、左侧和右侧子节点的值。
import { defaultCompare, Compare, swap } from '../util'
/**
* 最小堆类
* 完全二叉树,根节点最小的堆叫做最小堆
* 在二叉堆中,每个子节点都要大于等于父节点
* @export
* @class MinHeap
*/
export class MinHeap {
constructor(compareFn = defaultCompare) {
this.compareFn = compareFn;
this.heap = []; // 使用数组来存储数据,通过索引值检索父节点、左侧和右侧子节点的值。
}
getLeftIndex(index) {
return 2 * index + 1;
}
getRightIndex(index) {
return 2 * index + 2;
}
getParentIndex(index) {
if (index === 0) {
return undefined;
}
return Math.floor((index - 1) / 2)
}
/**
* 向堆中插入值
* 指将值插入堆的底部叶节点(数组的最后一个位置)
* @param {*} value
* @memberof MinHeap
*/
insert(value) {
if (value !== null) {
this.heap.push(value);
this.siftUp(this.heap.length - 1); // 将这个值和它的父节点进行交换,直到父节点小于这个插入的值。
return true;
}
return false;
}
/**
* 上移操作,维护堆的结构
* 将这个值和它的父节点进行交换,直到父节点小于这个插入的值。
* @param {*} index
* @memberof MinHeap
*/
siftUp(index) {
let parent = this.getParentIndex(index); // 获得父节点的索引
while( index > 0 && this.compareFn(this.heap[parent], this.heap[index]) === Compare.BIGGER_THAN) {
swap(this.heap, parent, index);
index = parent; // 往上替换
}
}
size() {
return this.heap.length;
}
isEmpty() {
return this.size() === 0;
}
/**
* 从堆中找到最小值或最大值
* 在最小堆中,最小值总是位于数组的第一个位置(堆的根节点)
* @memberof MinHeap
*/
findMinimum() {
return this.isEmpty() ? undefined : this.heap[0];
}
/**
* 移除最小值表示移除数组中的第一个元素(堆的根节点)。
* 在移除后,我们将堆的最后一个元素移动至根部并执行 siftDown 函数,表示我们将交换元素直到堆的结构正常。
* @memberof MinHeap
*/
extract() {
if(this.isEmpty()) {
return undefined;
}
if (this.size() === 1) {
return this.heap.shift();
}
const removedValue = this.heap.shift();
this.siftDown(0);
return removedValue;
}
/**
* 下移操作,维护堆的结构
* @param {*} index 移除元素的位置
* @memberof MinHeap
*/
siftDown(index) {
let element = index; // 将 index 复制到 element 变量中
const left = this.getLeftIndex(index);
const right = this.getRightIndex(index);
const size = this.size();
// 如果元素比左侧节点要小,且 index 合法。
if (left < size && this.compareFn(this.heap[element], this.heap[left]) === Compare.BIGGER_THAN) {
element = left;
}
// 如果元素比右侧节点要小,且 index 合法。
if (right < size && this.compareFn(this.heap[element], this.heap[right] === Compare.BIGGER_THAN)) {
element = right;
}
if (index !== element) {
swap(this.heap, index, element);
this.siftDown(element); // 向下移动
}
}
}
堆的应用
在程序中,堆用于动态分配和释放程序中所使用的对象。在以下情况中调用堆操作:
- 事先不知道程序所需对象的数量和大小。
- 对象太大,不适合使用堆栈分配器。
关于堆、栈、队列的可视化描述:
